ปัญหาสามารถแก้ไขได้ใน O (polylog (b))
เรากำหนดf(d, n)ให้เป็นจำนวนเต็มสูงสุดถึง d หลักทศนิยมที่มีผลรวมหลักน้อยกว่าหรือเท่ากับ n จะเห็นได้ว่าฟังก์ชั่นนี้ได้รับจากสูตร

มาฟังก์ชั่นนี้โดยเริ่มจากสิ่งที่ง่ายกว่ากัน
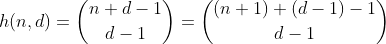
ฟังก์ชั่น h นับจำนวนวิธีในการเลือกองค์ประกอบ d - 1 จากชุดที่ประกอบด้วยองค์ประกอบที่แตกต่างกัน n + 1 นอกจากนี้ยังมีวิธีการแบ่งพาร์ติชัน n เป็น d ถังขยะซึ่งสามารถมองเห็นได้ง่ายโดยการสร้างรั้ว d - 1 รั้วรอบ ๆ n และสรุปแต่ละส่วนที่แยกจากกัน ตัวอย่างสำหรับ n = 2, d = 3 ':
3-choose-2 fences number
-----------------------------------
11 ||11 002
12 |1|1 011
13 |11| 020
22 1||1 101
23 1|1| 110
33 11|| 200
ดังนั้น h จึงนับจำนวนทั้งหมดที่มีผลรวมหลักของ n และ d หลัก ยกเว้นจะใช้งานได้กับ n น้อยกว่า 10 เนื่องจากตัวเลขจะถูก จำกัด ที่ 0 - 9 ในการแก้ไขปัญหานี้สำหรับค่า 10 - 19 เราจำเป็นต้องลบจำนวนพาร์ติชันที่มีหนึ่งถังที่มีหมายเลขมากกว่า 9 ซึ่งฉันจะเรียกถังขยะที่ overflown นับจากนี้เป็นต้นไป
คำนี้สามารถคำนวณได้โดยการนำ h กลับมาใช้ใหม่ด้วยวิธีต่อไปนี้ เรานับจำนวนวิธีที่จะแบ่งพาร์ติชัน n - 10 จากนั้นเลือกหนึ่งในถังขยะเพื่อใส่ 10 เข้าไปซึ่งส่งผลให้จำนวนพาร์ติชันที่มีถังขยะหนึ่งอัน ผลลัพธ์คือฟังก์ชันเบื้องต้นต่อไปนี้
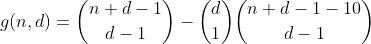
เราทำแบบนี้ต่อไปสำหรับ n น้อยกว่าหรือเท่ากับ 29 โดยนับวิธีการแบ่งพาร์ติชัน n - 20 ทั้งหมดจากนั้นเลือก 2 ถังขยะที่เราใส่ 10 ลงไปดังนั้นจึงนับจำนวนพาร์ติชันที่มีถังขยะ 2 อันล้น
แต่ ณ จุดนี้เราต้องระวังเพราะเรานับพาร์ติชั่นที่มีถังขยะ 2 อันในระยะก่อนหน้า ไม่เพียงแค่นั้น แต่ที่จริงแล้วเรานับพวกเขาสองครั้ง ลองใช้ตัวอย่างและดูพาร์ติชั่น (10,0,11) ด้วยผลรวม 21 ในเทอมก่อนหน้าเราลบ 10 คำนวณพาร์ติชั่นทั้งหมดที่เหลือ 11 และใส่ 10 เข้าไปในหนึ่งใน 3 ถังขยะ แต่พาร์ติชันนี้สามารถเข้าถึงได้ด้วยวิธีใดวิธีหนึ่งจากสองวิธี:
(10, 0, 1) => (10, 0, 11)
(0, 0, 11) => (10, 0, 11)
เนื่องจากเรายังนับพาร์ติชันเหล่านี้อีกครั้งในเทอมแรกการนับรวมของพาร์ติชันที่มีจำนวน 2 ถังที่ overflown เท่ากับ 1 - 2 = -1 ดังนั้นเราต้องนับอีกครั้งโดยการเพิ่มคำถัดไป
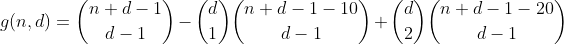
เมื่อคิดเกี่ยวกับเรื่องนี้อีกเล็กน้อยเราจะค้นพบว่าจำนวนครั้งที่พาร์ติชันที่มีจำนวนของช่องเก็บข้อมูล overflown จำนวนเฉพาะถูกนับในคำเฉพาะสามารถแสดงได้โดยตารางต่อไปนี้ (คอลัมน์ i หมายถึงคำว่า i พาร์ติชัน j แถวกับ j overflown ถังขยะ)
1 0 0 0 0 0 . .
1 1 0 0 0 0 . .
1 2 1 0 0 0 . .
1 4 6 4 1 0 . .
. . . . . .
. . . . . .
ใช่มันคือสามเหลี่ยม Pascals สิ่งเดียวที่เราสนใจคือสิ่งที่อยู่ในแถว / คอลัมน์แรกนั่นคือจำนวนพาร์ติชั่นที่มีถังขยะล้นศูนย์ และเนื่องจากผลรวมสลับของทุกแถว แต่ค่าแรกเท่ากับ 0 (เช่น 1 - 4 + 6 - 4 + 1 = 0) นั่นคือวิธีที่เรากำจัดพวกมันและมาถึงสูตรสุดท้าย
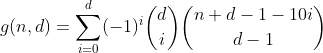
ฟังก์ชั่นนี้นับจำนวนทั้งหมดด้วยตัวเลข d ซึ่งมีตัวเลขผลรวมเป็น n
ทีนี้แล้วตัวเลขที่มีผลรวมตัวเลขน้อยกว่า n เราสามารถใช้การเกิดซ้ำแบบมาตรฐานสำหรับทวินามรวมทั้งการโต้แย้งแบบอุปนัยเพื่อแสดงให้เห็นว่า
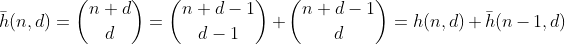
นับจำนวนพาร์ติชันด้วยผลรวมดิจิตที่ n มากที่สุด และจาก f นี้สามารถหาได้โดยใช้อาร์กิวเมนต์เดียวกันกับ g
การใช้สูตรนี้เราสามารถหาจำนวนของตัวเลขจำนวนมากในช่วงเวลาจาก 8,000 ถึง 8999 ในกรณี1000 - f(3, 20)นี้เพราะมีตัวเลขนับพันในช่วงเวลานี้และเราต้องลบจำนวนตัวเลขที่มีผลรวมหลักน้อยกว่าหรือเท่ากับ 28 ในขณะที่คำนึงถึงตัวเลขหลักแรกที่มีส่วน 8 ถึงผลรวมหลัก
เป็นตัวอย่างที่ซับซ้อนมากขึ้นมาดูที่จำนวนของตัวเลขหนักในช่วง 1234..5678 เราสามารถเริ่มจาก 1234 ถึง 1240 ในขั้นตอนที่ 1 จากนั้นเราไปจาก 1240 ถึง 1300 ในขั้นตอนที่ 10 สูตรข้างต้นให้จำนวนตัวเลขหนักในแต่ละช่วงเวลาดังกล่าว:
1240..1249: 10 - f(1, 28 - (1+2+4))
1250..1259: 10 - f(1, 28 - (1+2+5))
1260..1269: 10 - f(1, 28 - (1+2+6))
1270..1279: 10 - f(1, 28 - (1+2+7))
1280..1289: 10 - f(1, 28 - (1+2+8))
1290..1299: 10 - f(1, 28 - (1+2+9))
ตอนนี้เราไปจาก 1300 ถึง 2000 ในขั้นตอน 100:
1300..1399: 100 - f(2, 28 - (1+3))
1400..1499: 100 - f(2, 28 - (1+4))
1500..1599: 100 - f(2, 28 - (1+5))
1600..1699: 100 - f(2, 28 - (1+6))
1700..1799: 100 - f(2, 28 - (1+7))
1800..1899: 100 - f(2, 28 - (1+8))
1900..1999: 100 - f(2, 28 - (1+9))
จาก 2000 ถึง 5,000 ในขั้นตอน 1,000:
2000..2999: 1000 - f(3, 28 - 2)
3000..3999: 1000 - f(3, 28 - 3)
4000..4999: 1000 - f(3, 28 - 4)
ตอนนี้เราต้องลดขนาดขั้นตอนอีกครั้งจาก 5,000 เป็น 5600 ในขั้นตอนที่ 100 จาก 5600 เป็น 5670 ในขั้นตอนที่ 10 และสุดท้ายจาก 5670 เป็น 5678 ในขั้นตอนที่ 1
ตัวอย่างการใช้งาน Python (ซึ่งได้รับการเพิ่มประสิทธิภาพเล็กน้อยและการทดสอบในขณะเดียวกัน):
def binomial(n, k):
if k < 0 or k > n:
return 0
result = 1
for i in range(k):
result *= n - i
result //= i + 1
return result
binomial_lut = [
[1],
[1, -1],
[1, -2, 1],
[1, -3, 3, -1],
[1, -4, 6, -4, 1],
[1, -5, 10, -10, 5, -1],
[1, -6, 15, -20, 15, -6, 1],
[1, -7, 21, -35, 35, -21, 7, -1],
[1, -8, 28, -56, 70, -56, 28, -8, 1],
[1, -9, 36, -84, 126, -126, 84, -36, 9, -1]]
def f(d, n):
return sum(binomial_lut[d][i] * binomial(n + d - 10*i, d)
for i in range(d + 1))
def digits(i):
d = map(int, str(i))
d.reverse()
return d
def heavy(a, b):
b += 1
a_digits = digits(a)
b_digits = digits(b)
a_digits = a_digits + [0] * (len(b_digits) - len(a_digits))
max_digits = next(i for i in range(len(a_digits) - 1, -1, -1)
if a_digits[i] != b_digits[i])
a_digits = digits(a)
count = 0
digit = 0
while digit < max_digits:
while a_digits[digit] == 0:
digit += 1
inc = 10 ** digit
for i in range(10 - a_digits[digit]):
if a + inc > b:
break
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
while a < b:
while digit and a_digits[digit] == b_digits[digit]:
digit -= 1
inc = 10 ** digit
for i in range(b_digits[digit] - a_digits[digit]):
count += inc - f(digit, 7 * len(a_digits) - sum(a_digits))
a += inc
a_digits = digits(a)
return count
แก้ไข : แทนที่รหัสด้วยเวอร์ชันที่ได้รับการปรับปรุงแล้ว ยังแก้ไขบางกรณีมุมในขณะที่ฉันอยู่ที่มัน heavy(1234, 100000000)ใช้เวลาประมาณหนึ่งมิลลิวินาทีบนเครื่องของฉัน
