ทำไมแบบจำลองประตูไม่สามารถอธิบายการควอนตัมควอนตัมได้?

นี่เป็นคำถามที่ฉันได้รับแรงบันดาลใจให้ถามตามคำถามนี้ซึ่งตั้งข้อสังเกตว่าการหลอมควอนตัมเป็นแบบจำลองที่แตกต่างไปจากเดิมอย่างสิ้นเชิงสำหรับการคำนวณมากกว่าแบบจำลองวงจรปกติ ฉันเคยได้ยินเรื่องนี้มาก่อนและมันเป็นความเข้าใจของฉันว่าแบบจำลองเกทไม่สามารถใช้ได้กับการหลอมควอนตัม แต่ฉันไม่เคยเข้าใจเลยว่าทำไมถึงเป็นเช่นนั้น ตามที่ฉันเข้าใจจากการพูดคุยหลายครั้ง (บางคนเขียนโดย D-wave ด้วยตัวเอง!) ความจริงที่ว่าผู้ค้ายาถูกกักขังอยู่ในบทละครมิลโตเนียนที่เล่นโดยเฉพาะ

Quantum Annealer เช่นเครื่อง D-Wave เป็นตัวแทนทางกายภาพของโมเดล Ising และมี 'ปัญหา' Hamiltonian ของรูปแบบ

โดยพื้นฐานแล้วปัญหาที่จะแก้ไขถูกแมปกับมิลโตเนียนข้างต้น ระบบเริ่มต้นด้วย Hamiltonian และพารามิเตอร์การอบsใช้เพื่อทำแผนที่เริ่มต้น Hamiltonian H Iกับปัญหา Hamiltonian H Pโดยใช้H ( s ) = ( 1 - s ) H ฉัน + s H P$H_I = \sum_{J=1}^nh'_j\sigma_j^x$$s$$H_I$$H_P$$H\left(s\right) = \left(1-s\right)H_I + sH_P$

เช่นนี้เป็นหลอมกระบวนการที่จะทำอย่างช้า ๆ พอที่จะอยู่ใกล้กับสภาพพื้นดินของระบบในขณะที่แฮมิลตันจะแตกต่างกันกับที่ของปัญหาที่เกิดขึ้นโดยใช้อุโมงค์เพื่อเข้าพักที่อยู่ใกล้กับสภาพพื้นดินที่อธิบายไว้ในคำตอบของชัยนาท

ทีนี้ทำไมมันไม่สามารถใช้อธิบายแบบจำลองประตูได้? ดังกล่าวข้างต้นเป็นกำลังสองข้อ จำกัด เพิ่มประสิทธิภาพไบนารี (QUBO)ปัญหาซึ่งเป็น NP-ยาก ... อันที่จริงนี่เป็นบทความที่ทำแผนที่จำนวนของปัญหา NP กับรูปแบบ ปัญหาใด ๆ ใน NP สามารถแมปกับปัญหา NP-hard ใด ๆ ในเวลาพหุนามและการแยกตัวประกอบจำนวนเต็มเป็นปัญหา NP แน่นอน

อุณหภูมิไม่เป็นศูนย์ดังนั้นมันจะไม่อยู่ในสภาพพื้นดินตลอดการหลอมและผลก็คือวิธีแก้ปัญหายังคงเป็นเพียงค่าประมาณเท่านั้น หรือในแง่ที่แตกต่างกันความน่าจะเป็นของความล้มเหลวสูงกว่าครึ่ง (ไม่มีที่ไหนเลยใกล้จะมีความน่าจะเป็นที่ดีของความสำเร็จเมื่อเทียบกับสิ่งที่ QC สากลพิจารณาว่า 'เหมาะสม' - ตัดสินจากกราฟที่ฉันเคยเห็น เครื่องปัจจุบันอยู่ที่ประมาณและสิ่งนี้จะยิ่งแย่ลงเมื่อขนาดที่เพิ่มขึ้น) และอัลกอริธึมหลอมไม่ผิดพลาด เลย ดังนั้นจึงไม่มีทางรู้ได้ว่าคุณมีวิธีแก้ปัญหาที่ถูกต้องกับบางสิ่งเช่นการแยกตัวประกอบจำนวนเต็ม$0.2\%$

สิ่งที่มัน (โดยหลักการ) ไม่ได้ใกล้เคียงกับผลลัพธ์ที่แน่นอนอย่างรวดเร็วมาก แต่สิ่งนี้ไม่ได้ช่วยอะไรที่จำเป็นต้องได้ผลลัพธ์ที่แน่นอนว่าเปลี่ยนจาก 'เกือบถูกต้อง' เป็น 'ถูกต้อง' ยังคงเป็นเรื่องยากมาก ( กล่าวคือยังคงเป็นปัญหาทั่วไปโดยทั่วไปเมื่อปัญหาดั้งเดิมอยู่ในปัญหา NP) ในกรณีนี้เนื่องจากพารามิเตอร์ที่ / ให้คำตอบที่ 'เกือบถูกต้อง' ไม่จำเป็นต้องกระจายไปทุกที่ใกล้กับพารามิเตอร์ที่ให้ ทางออกที่ถูกต้อง

แก้ไขเพื่อความกระจ่าง: สิ่งนี้หมายความว่าตัวควอนตัม annealer (QA) ยังคงใช้เวลาชี้แจง (แม้ว่าอาจจะเป็นเวลาเร็วแทน) ในการแก้ปัญหา NP เช่นตัวคูณจำนวนเต็มที่ QC สากลให้ความเร็วแบบเอ็กซ์โพเนนเชียล ปัญหาในเวลาโพลี นี่คือสิ่งที่แสดงถึงการควบคุมคุณภาพไม่สามารถจำลอง QC สากลในเวลาโพลี (มิฉะนั้นมันสามารถแก้ปัญหาในเวลาโพลีที่มันไม่สามารถ) ตามที่ระบุไว้ในความคิดเห็นสิ่งนี้ไม่เหมือนกับการบอกว่า QA ไม่สามารถให้ความเร็วเท่ากันในปัญหาอื่น ๆ เช่นการค้นหาฐานข้อมูล

การหลอมมากขึ้นของชั้นเชิงแบบอะนาล็อก

ส่วนสำคัญคือคุณมีฟังก์ชั่นแปลก ๆ ที่คุณต้องการปรับให้เหมาะสม ดังนั้นคุณจะเด้งรอบ ในตอนแรก " อุณหภูมิ " สูงมากเช่นที่จุดที่เลือกสามารถเด้งได้มาก จากนั้นเมื่ออัลกอริทึม " เย็นลง " อุณหภูมิจะลดลงและการสะท้อนกลับจะรุนแรงน้อยลง

ในที่สุดมันก็ตั้งหลักแหล่งไปยังเมืองออพติม่าซึ่งเป็นที่นิยมในระดับโลก

นี่คือภาพเคลื่อนไหวสำหรับการหลอมจำลอง (ไม่ใช่ควอนตัม):

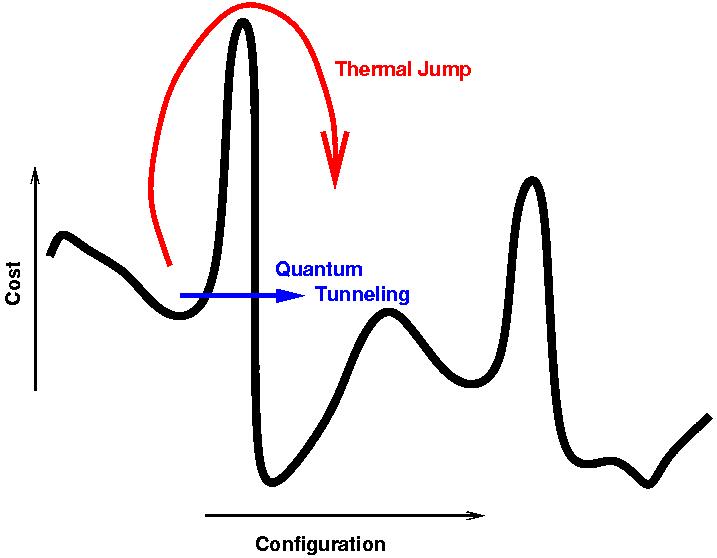
แต่มันก็เป็นแนวคิดเดียวกันในการหลอมควอนตัม :

ในทางตรงกันข้ามเกต - ลอจิกนั้นมีความดิจิตอลมากกว่าอนาล็อก มันเกี่ยวข้องกับ qubits และการดำเนินการเชิงตรรกะมากกว่าเพียงแค่การค้นหาผลลัพธ์หลังจากการกระเด้งกระดอนรอบ ๆ