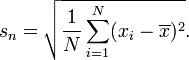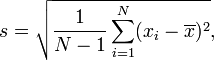เหตุใดโรงเรียนในสหรัฐอเมริกาและสหราชอาณาจักรจึงสอนวิธีต่างๆในการคำนวณส่วนเบี่ยงเบนมาตรฐาน

15

ตามที่ฉันเข้าใจโรงเรียนในสหราชอาณาจักรสอนว่าการเบี่ยงเบนมาตรฐานนั้นใช้โดย:

$ข้อความแสดงแทน$

ในขณะที่โรงเรียนของเราสอน:

$ข้อความแสดงแทน$

(ในระดับพื้นฐานอยู่แล้ว)

สิ่งนี้ทำให้นักเรียนของฉันมีปัญหาหลายอย่างในอดีตเมื่อพวกเขาค้นหาบนอินเทอร์เน็ต แต่พบคำอธิบายที่ผิด

ทำไมถึงแตกต่าง

ด้วยชุดข้อมูลอย่างง่ายบอกว่ามีค่า 10 ระดับข้อผิดพลาดระดับใดที่จะเกิดขึ้นหากใช้วิธีการที่ไม่ถูกต้อง (เช่นในการสอบ)?

— เอมัส
แหล่งที่มา

4

ฉันไม่แน่ใจว่าการอธิบายลักษณะอย่างใดอย่างหนึ่งเป็นสูตร 'ผิด' เป็นวิธีที่จะเข้าใจปัญหาหรือไม่ เป็นเพียงว่าตัวที่สองนั้น 'ดีกว่า' ในแง่ที่ว่ามันเป็นตัวประมาณค่าที่ไม่เอนเอียงของค่าเบี่ยงเบนมาตรฐานที่แท้จริง ดังนั้นหากคุณสนใจค่าประมาณที่ไม่เอนเอียงค่าที่สองคือ 'ดีกว่า' / 'ถูกต้อง'

ฉันอธิบายลักษณะของสูตรว่า "ผิด" อย่างหมดจดในแง่ที่ว่าในการสอบถ้าคุณใช้สูตรที่ไม่ได้ถูกสั่งโดยหลักสูตรคุณจะต้องจบด้วยคำตอบที่ "ผิด" บวกถ้าค่าไม่ใช่ตัวอย่างประชากรต่อ se แน่นอนว่าสูตรแรกให้ค่าที่ถูกต้องมากขึ้น

— Amos

14

ศรีกันต์ฉันไม่คิดว่าคนที่สองเป็นผู้ประเมินที่เป็นกลาง กำลังสองของมันเป็นตัวประมาณค่าความแปรปรวนที่แท้จริง อย่างไรก็ตามความไม่เท่าเทียมของเจนเซ่นนั้นกำหนดว่าความคาดหวังของฟังก์ชัน curvilinear ของตัวแปรสุ่มนั้นไม่เหมือนกับฟังก์ชันของความคาดหวังของตัวแปรสุ่ม ดังนั้นสูตรที่สองจึงไม่สามารถเป็นตัวประมาณค่าความเบี่ยงเบนมาตรฐานที่แท้จริงได้

— Andrew Robinson

สำหรับการอ้างอิงโยง: มันถูกถามด้วย @ m.SE ...

— JM ไม่ใช่นักสถิติ

4

โรงเรียนใด ๆ ในสหรัฐฯที่ใช้ข้อความระดับต้น ๆ ที่เป็นที่นิยมมากโดย Freedman, Pisani, & Purves กำลังใช้สูตรแรก ( ) ดังนั้นจึงดูเหมือนว่าไม่ถูกต้องที่จะอธิบายลักษณะนี้เป็นความแตกต่างระหว่างสหรัฐฯกับอังกฤษ

s_{n}

$s_n$

— whuber

18

สูตรแรกคือค่าเบี่ยงเบนมาตรฐานประชากรและสูตรที่สองคือค่าเบี่ยงเบนมาตรฐานตัวอย่าง สูตรที่สองเกี่ยวข้องกับตัวประมาณค่าความแปรปรวนแบบเป็นกลาง - ดูวิกิพีเดียสำหรับรายละเอียดเพิ่มเติม

ฉันคิดว่า (ที่นี่) ในสหราชอาณาจักรพวกเขาไม่ได้แยกความแตกต่างระหว่างกลุ่มตัวอย่างและประชากรในโรงเรียนมัธยม แน่นอนว่าพวกเขาไม่ได้สัมผัสแนวคิดเช่นเครื่องมือประเมินลำเอียง

— csgillespie
แหล่งที่มา

4

โคลินผู้ประมาณความเบี่ยงเบนมาตรฐานที่เป็นกลางไม่ได้เป็นตัวแทนรูปแบบปิดในกรณีทั่วไป สิ่งที่มีอยู่คือตัวประมาณค่าที่ไม่เอนเอียงของ ความแปรปรวน (s 2 ในกรณีนี้) น่าสังเกตว่าทั้งคู่เป็นตัวประมาณความแปรปรวนของประชากรอย่างต่อเนื่องโดยทฤษฎีการทำแผนที่แบบต่อเนื่องเป็นตัวประมาณค่าความเบี่ยงเบนมาตรฐานสองตัว จุดที่เกี่ยวข้องคือ s n 2 มี MSE ต่ำกว่า s 2 ข้อได้เปรียบเพิ่มเติมจากการจัดเก็บภาษีที่เป็นกลางเป็นสิ่งที่พิสูจน์ได้

— Mornington

@Tirthankar - เลอะเทอะมากกับฉัน ฉันเปลี่ยนคำตอบเล็กน้อย ขอบคุณ

— csgillespie

2

เท่าที่ฉันจำได้ฉันได้รับการสอนการคำนวณ 'ตัวอย่าง' ในวิชาคณิตศาสตร์และวิทยาศาสตร์ GCSE (อายุ 14-16 ปี) และความแตกต่างระหว่างประชากรและกลุ่มตัวอย่างและการวัดความแปรปรวนที่เกี่ยวข้องของพวกเขาถูกครอบคลุม อายุ 16-18) ดังนั้นฉันไม่แน่ใจว่านี่เป็นความแตกต่างง่ายๆระหว่างอังกฤษ / สหรัฐอเมริกา

— Freya Harrison

11

เพราะไม่มีใครตอบคำถามสุดท้าย - กล่าวคือเพื่อหาปริมาณความแตกต่างระหว่างสองสูตร - มาดูแลกันดีกว่า

ด้วยเหตุผลหลายประการมีความเหมาะสมที่จะเปรียบเทียบส่วนเบี่ยงเบนมาตรฐานในแง่ของอัตราส่วนแทนที่จะเป็นความแตกต่าง อัตราส่วนคือ

s_{n} / s = \sqrt{\frac{N - 1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2 N} .

$s_n / s = \sqrt{\frac{N-1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2N}.$

$|\binom{1/2}{2}N^{-2}|$ $1 / (8 N^2)$ $N$ $2$

ทันทีที่การประมาณค่า SD ทั้งสองอยู่ภายใน (ประมาณ) 10% ของกันและกันเมื่อเกิน , ภายใน 5% เมื่อเกินและอื่น ๆ เห็นได้ชัดว่าด้วยเหตุผลหลายประการความแตกต่างเหล่านี้มีขนาดเล็กจนไม่สำคัญว่าจะใช้สูตรใดโดยเฉพาะอย่างยิ่งเมื่อ SD มีไว้เพื่ออธิบายการแพร่กระจายของข้อมูลหรือทำการประเมินเชิงกึ่งปริมาณหรือการคาดการณ์ -99.7 กฎของหัวแม่มือ) ความแตกต่างมีความสำคัญน้อยลงเมื่อเปรียบเทียบ $N$ $5$ $N$ $10$ SDs เช่นเมื่อเปรียบเทียบการกระจายของชุดข้อมูลสองชุด (เมื่อชุดข้อมูลมีค่าเท่ากันความคลาดเคลื่อนจะหายไปอย่างมีประสิทธิภาพและสูตรทั้งสองนำไปสู่ข้อสรุปที่เหมือนกัน) เนื้อหาเหล่านี้เป็นรูปแบบของการให้เหตุผลที่เราพยายามสอนนักเรียนเริ่มต้นดังนั้นหากนักเรียนกังวลว่าจะใช้สูตรใด นั่นอาจเป็นสัญญาณว่าข้อความหรือชั้นเรียนไม่สามารถเน้นสิ่งที่สำคัญจริงๆ

เราอาจจะต้องการให้ความสนใจบางอย่างกับกรณีของขนาดเล็กมากNที่นี่ผู้คนอาจใช้การทดสอบแทนการทดสอบเป็นต้น ในกรณีที่ว่ามันเป็นสิ่งสำคัญที่จะจ้างแล้วแต่จำนวนใดสูตรสำหรับค่าเบี่ยงเบนมาตรฐานจะถูกใช้โดยตารางหนึ่งหรือซอฟแวร์ (นี่ไม่ใช่เรื่องของหนึ่งสูตรว่าผิดหรือถูกต้องมันเป็นเพียงความต้องการที่สอดคล้องกัน) ตารางส่วนใหญ่ใช้ไม่ใช่ : นี่เป็นที่เดียวในหลักสูตรประถมที่ข้อความและครูต้องชัดเจนเกี่ยวกับสูตรใด ใช้. $N$ $t$ $z$ $s$ $s_n$

— whuber
แหล่งที่มา

6

นี่คือการแก้ไขของเบสเซิล รุ่นเรามีการแสดงสูตรสำหรับค่าเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่างที่ UK รุ่นดังกล่าวข้างต้นเป็นส่วนเบี่ยงเบนมาตรฐานของกลุ่มตัวอย่าง

— กก Copsey
แหล่งที่มา

5

ฉันไม่แน่ใจว่านี่เป็นปัญหาของสหรัฐฯและอังกฤษอย่างแท้จริง ส่วนที่เหลือของหน้านี้คัดลอกมาจากคำถามที่พบบ่อย ( http://www.graphpad.com/faq/viewfaq.cfm?faq=1383 )

วิธีการคำนวณ SD ด้วย n-1 ในตัวหาร

คำนวณกำลังสองของความแตกต่างระหว่างแต่ละค่าและค่าเฉลี่ยตัวอย่าง
เพิ่มค่าเหล่านั้นขึ้น
หารผลรวมด้วย n-1 ผลลัพธ์ถูกเรียกว่าความแปรปรวน
นำสแควร์รูทไปหาค่าเบี่ยงเบนมาตรฐาน

ทำไมต้อง n-1

ทำไมหารด้วย n-1 มากกว่า n เมื่อคำนวณส่วนเบี่ยงเบนมาตรฐาน ในขั้นตอนที่ 1 คุณคำนวณความแตกต่างระหว่างแต่ละค่าและค่าเฉลี่ยของค่าเหล่านั้น คุณไม่รู้ค่าเฉลี่ยที่แท้จริงของประชากร ทั้งหมดที่คุณรู้คือค่าเฉลี่ยของตัวอย่างของคุณ ยกเว้นกรณีที่หาได้ยากซึ่งค่าเฉลี่ยตัวอย่างเกิดขึ้นเท่ากับค่าเฉลี่ยประชากรข้อมูลจะใกล้เคียงกับค่าเฉลี่ยตัวอย่างมากกว่าค่าเฉลี่ยประชากรจริง ดังนั้นค่าที่คุณคำนวณในขั้นตอนที่ 2 อาจจะเล็กกว่าเล็กน้อย (และไม่สามารถมีขนาดใหญ่กว่า) ได้ถ้าคุณใช้ค่าเฉลี่ยประชากรจริงในขั้นตอนที่ 1 เมื่อต้องการทำสิ่งนี้ให้หารด้วย n-1 แทน กว่า nv สิ่งนี้เรียกว่าการแก้ไขของเบสเซล

แต่ทำไมต้อง n-1 หากคุณรู้ค่าเฉลี่ยตัวอย่างและทั้งหมดยกเว้นค่าใดค่าหนึ่งคุณสามารถคำนวณได้ว่าค่าสุดท้ายนั้นต้องเป็นเท่าใด นักสถิติกล่าวว่ามีองศาอิสระ n-1

เมื่อใดที่ควรคำนวณ SD ด้วยตัวส่วนของ n แทน n-1

หนังสือสถิติมักแสดงสมการสองอันเพื่อคำนวณ SD หนึ่งรายการที่ใช้ n และอีกอันใช้ n-1 ในตัวส่วน เครื่องคิดเลขบางตัวมีสองปุ่ม

สมการ n-1 ถูกใช้ในสถานการณ์ทั่วไปที่คุณกำลังวิเคราะห์ตัวอย่างของข้อมูลและต้องการสรุปโดยทั่วไป SD ที่คำนวณด้วยวิธีนี้ (โดยมี n-1 ในตัวส่วน) เป็นการคาดเดาที่ดีที่สุดของคุณสำหรับค่าของ SD ในประชากรโดยรวม

หากคุณเพียงต้องการหาปริมาณความแปรปรวนในชุดข้อมูลหนึ่ง ๆ และไม่ได้วางแผนที่จะคาดการณ์เพื่อให้ได้ข้อสรุปที่กว้างขึ้นคุณสามารถคำนวณ SD โดยใช้ n ในตัวหาร SD ที่ได้คือ SD ของค่าเฉพาะเหล่านั้น มันไม่มีเหตุผลที่จะคำนวณ SD ด้วยวิธีนี้หากคุณต้องการประมาณค่า SD ของประชากรที่ได้รับคะแนนเหล่านั้น มันสมเหตุสมผลที่จะใช้ n ในตัวหารเมื่อไม่มีการสุ่มตัวอย่างจากประชากรไม่มีความปรารถนาที่จะสรุปโดยทั่วไป

เป้าหมายของวิทยาศาสตร์นั้นมักจะพูดคุยกันเสมอดังนั้นไม่ควรใช้สมการกับ n ในตัวส่วน ตัวอย่างเดียวที่ฉันสามารถนึกได้ว่ามันจะเข้าท่าอย่างไรในการหาปริมาณความแปรปรวนระหว่างคะแนนสอบ แต่ที่ดีกว่ามากคือการแสดงกระจายของคะแนนทุกคะแนนหรือฮิสโตแกรมการกระจายความถี่

— Harvey Motulsky
แหล่งที่มา

1

ฉันไม่ได้บอกว่ามันเป็นฉันแค่อยากรู้ว่าทำไมความแตกต่างดังกล่าวอาจเกิดขึ้นระดับของข้อผิดพลาดตามคำแนะนำที่ผิดอาจให้และว่ามีคำอธิบายที่เหมาะสมของความแตกต่างที่ฉันสามารถให้กับนักเรียนของฉัน .

— Amos

@harvey - ลิงก์นั้นตาย

— baxx

1

@ แบ็กซ์ .. ขอบคุณที่ชี้ให้เห็น แก้ไขแล้ว.

— Harvey Motulsky

3

เนื่องจาก N คือจำนวนคะแนนในชุดข้อมูลเราสามารถโต้แย้งได้ว่าการคำนวณค่าเฉลี่ยได้ลดระดับความเป็นอิสระในข้อมูลที่กำหนดโดยหนึ่ง (ตั้งแต่มีการแนะนำการพึ่งพาชุดข้อมูล) ดังนั้นจึงควรใช้ N -1 เมื่อประมาณค่าเบี่ยงเบนมาตรฐานจากชุดข้อมูลที่หนึ่งต้องประเมินค่าเฉลี่ยก่อน

— Benjamin Bannier
แหล่งที่มา