ทฤษฎีบทของเบย์คืออะไร

อะไรคือความคิดหลักที่เป็นแนวความคิดที่เกี่ยวข้องกับทฤษฎีบท Bayes' ? ฉันไม่ได้ขอการแปลงสัญกรณ์ทางคณิตศาสตร์ที่ซับซ้อน

ทฤษฎีบทของเบย์นั้นค่อนข้างง่าย แต่ผลลัพธ์พื้นฐานของทฤษฎีความน่าจะเป็นที่ช่วยให้การคำนวณความน่าจะเป็นตามเงื่อนไขบางอย่าง ความน่าจะเป็นแบบมีเงื่อนไขเป็นเพียงความน่าจะเป็นที่สะท้อนอิทธิพลของเหตุการณ์หนึ่งต่อความน่าจะเป็นของเหตุการณ์อื่น

เพียงแค่ใส่ในรูปแบบที่มีชื่อเสียงที่สุดมันระบุว่าความน่าจะเป็นของสมมติฐานที่ได้รับข้อมูลใหม่ ( P (H | D) ; เรียกว่าความน่าจะเป็นหลัง) เท่ากับสมการต่อไปนี้: ความน่าจะเป็นของข้อมูลที่สังเกตได้จากสมมติฐานP (D | H) ; เรียกว่าความน่าจะเป็นตามเงื่อนไข) คูณความน่าจะเป็นของทฤษฎีที่เป็นจริงก่อนที่จะมีหลักฐานใหม่ ( P (H)เรียกว่าความน่าจะเป็นก่อนหน้าของ H) หารด้วยความน่าจะเป็นที่เห็นข้อมูลP (D ); เรียกว่าความน่าจะเป็นที่ขอบของ D)

สมการมีลักษณะดังนี้:

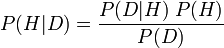
ความสำคัญของทฤษฎีบทเบย์เป็นส่วนใหญ่เนื่องจากการใช้งานที่เหมาะสมเป็นจุดของความขัดแย้งระหว่างโรงเรียนแห่งความคิดเกี่ยวกับความน่าจะเป็น สำหรับอัตวิสัยเบย์ (แปลว่าความน่าจะเป็นระดับความเชื่อตามอัตวิสัย) ทฤษฎีบทของเบส์เป็นรากฐานที่สำคัญสำหรับการทดสอบทฤษฎีการเลือกทฤษฎีและการปฏิบัติอื่น ๆ โดยการเสียบความน่าจะเป็นอัตนัยเข้ากับสมการและวิ่งไปกับมัน สำหรับนักความถี่ (ที่ตีความความน่าจะเป็นในการ จำกัด ความถี่สัมพัทธ์ ) การใช้ทฤษฎีบทของเบย์นี้เป็นการละเมิดและพวกเขามุ่งมั่นที่จะใช้นักบวชที่มีความหมาย (ไม่ใช่ส่วนตัว) ที่มีความหมาย

ฉันขอโทษ แต่ดูเหมือนว่าจะมีความสับสนบางอย่างที่นี่: เบส์ทฤษฎีบทไม่ได้ขึ้นสำหรับการอภิปรายของ neverending Bayesian- frequentistอภิปราย มันเป็นทฤษฎีบทที่สอดคล้องกับทั้งโรงเรียนแห่งความคิด (เนื่องจากมันสอดคล้องกับสัจพจน์ของความน่าจะเป็นของ Kolmogorov)

แน่นอนว่าทฤษฎีบทของเบย์เป็นแกนหลักของสถิติของเบย์ แต่ทฤษฎีบทนั้นเป็นสากล การปะทะกันระหว่างผู้ใช้บ่อยและไบเซียนส่วนใหญ่เกี่ยวข้องกับวิธีการแจกแจงก่อนหน้านี้ที่สามารถกำหนดหรือไม่

ดังนั้นหากคำถามเกี่ยวกับทฤษฎีบทของเบย์ (และไม่ใช่สถิติแบบเบย์):

ทฤษฎีบทของเบย์กำหนดวิธีที่เราสามารถคำนวณความน่าจะเป็นแบบมีเงื่อนไขเฉพาะ ลองนึกภาพตัวอย่างที่คุณรู้: ความน่าจะเป็นของใครบางคนที่มีอาการ A เนื่องจากพวกเขามีโรค X p (A | X) ความน่าจะเป็นของคนทั่วไปที่มีโรค X p (X) ความน่าจะเป็นของใครบางคนโดยทั่วไปที่มีอาการ A p (A) ด้วยข้อมูลทั้งสามชิ้นนี้คุณสามารถคำนวณความน่าจะเป็นของผู้ที่มีโรค X เนื่องจากพวกเขามี sympotm A p (X | A)

$P(A|B)$$P(B|A)$

$P(B|A)$$A$$P(\mbox{dice lands six})$$P(\mbox{dice lands six}|\mbox{dice lands even})$

คุณสามารถหาทฤษฎีบทของเบย์ได้ด้วยตนเองดังนี้ เริ่มต้นด้วยคำจำกัดความอัตราส่วนของความน่าจะเป็นแบบมีเงื่อนไข:

$P(B|A) = \frac{P(AB)}{P(A)}$

$P(AB)$$A$$B$$P(A)$$A$

$P(A|B)$

$P(A|B) = \frac{P(BA)}{P(B)}$

$P(AB) = P(BA)$$AB = BA$

$P(A|B) = \frac{P(AB)}{P(B)}$

$P(B|A)$$P(AB)$

$P(AB) = P(A|B)P(B)$

และเฮ้ presto:

$P(B|A) = \frac{P(A|B)P(B)}{P(A)}$

สำหรับประเด็นที่จะหมุนความน่าจะเป็นแบบมีเงื่อนไขในลักษณะนี้ให้พิจารณาตัวอย่างทั่วไปของการพยายามอนุมานความน่าจะเป็นที่ใครบางคนมีโรคเนื่องจากพวกเขามีอาการคือเรารู้ว่าพวกเขามีอาการ - เราสามารถทำได้ เห็นมัน - แต่เราไม่สามารถแน่ใจได้ว่าพวกเขามีโรคหรือไม่ ฉันจะเริ่มต้นด้วยสูตรและทำงานอีกครั้ง

$P(\mbox{disease}|\mbox{symptom}) = \frac{P(\mbox{symptom}|\mbox{disease})P(\mbox{disease})}{P(\mbox{symptom})}$

เพื่อที่จะทำให้มันออกมาคุณจะต้องรู้ถึงความน่าจะเป็นก่อนของอาการความน่าจะเป็นก่อนของโรค (กล่าวคืออาการและโรคที่พบได้บ่อยหรือหายาก) และความน่าจะเป็นที่ใครบางคนมีอาการ โรค (เช่นผ่านการทดสอบในห้องปฏิบัติการที่ต้องใช้เวลามาก)

มันอาจซับซ้อนกว่านี้มากเช่นถ้าคุณมีโรคและอาการหลายอย่าง แต่ความคิดก็เหมือนกัน โดยทั่วไปยิ่งขึ้นทฤษฎีบทของเบย์มักปรากฏถ้าคุณมีทฤษฎีความน่าจะเป็นของความสัมพันธ์ระหว่างสาเหตุ (เช่นโรค) และผลกระทบ (เช่นอาการ) และคุณจำเป็นต้องให้เหตุผลย้อนหลัง (เช่นคุณเห็นอาการบางอย่างที่คุณต้องการ เพื่ออนุมานโรคพื้นฐาน)

ทั้งสองมีโรงเรียนหลักของความคิดก็คือสถิติ: frequentist และคชกรรม

ทฤษฎีบทของเบย์นั้นเกี่ยวข้องกับสิ่งหลังและสามารถมองได้ว่าเป็นวิธีการทำความเข้าใจว่าความน่าจะเป็นที่ทฤษฎีนั้นจริงได้รับผลกระทบจากหลักฐานชิ้นใหม่ สิ่งนี้เรียกว่าความน่าจะเป็นแบบมีเงื่อนไข คุณอาจต้องการดูสิ่งนี้เพื่อจัดการกับคณิตศาสตร์

ฉันขอให้คุณมีความเข้าใจที่ลึกซึ้งมาก สมมติว่าคุณกำลังโยนเหรียญ 10 ครั้งและคุณจะได้รับ 8 หัวและ 2 ก้อย คำถามที่อยู่ในใจของคุณคือเหรียญนี้มีอคติต่อหัวหรือไม่

ตอนนี้ถ้าคุณไปตามคำจำกัดความดั้งเดิมหรือวิธีการความน่าจะเป็นบ่อยครั้งคุณอาจพูดได้ว่าเหรียญนั้นไม่เอนเอียงและนี่เป็นเหตุการณ์พิเศษ ดังนั้นคุณจะสรุปได้ว่าความเป็นไปได้ที่จะได้รับการโยนครั้งต่อไปเป็น 50% เช่นกัน

แต่สมมติว่าคุณเป็นชาวเบย์ คุณจะคิดว่าจริง ๆ แล้วเนื่องจากคุณมีจำนวนหัวที่สูงเป็นพิเศษเหรียญนั้นจึงมีอคติไปทางด้านหัว มีวิธีการคำนวณอคติที่เป็นไปได้นี้ คุณจะคำนวณพวกมันและเมื่อคุณโยนเหรียญในครั้งต่อไปคุณจะต้องเรียกหัว

ดังนั้นความน่าจะเป็นแบบเบย์คือเกี่ยวกับความเชื่อที่คุณพัฒนาตามข้อมูลที่คุณสังเกต ฉันหวังว่ามันง่ายพอ

ทฤษฎีบทของเบย์เกี่ยวข้องกับแนวคิดสองประการ ได้แก่ ความน่าจะเป็นและความน่าจะเป็น ความน่าจะเป็นพูดว่า: จากโมเดลนี้ผลลัพธ์เหล่านี้คือ ดังนั้น: รับเหรียญที่ยุติธรรมฉันจะได้หัว 50% ของเวลา Likelihood พูดว่า: จากผลลัพธ์เหล่านี้นี่คือสิ่งที่เราสามารถพูดเกี่ยวกับแบบจำลอง ดังนั้น: ถ้าคุณโยนเหรียญ 100 ครั้งและรับ 88 หัว (เพื่อยกตัวอย่างก่อนหน้าและทำให้สุดยอดมากขึ้น) ความเป็นไปได้ที่รูปแบบเหรียญที่ยุติธรรมนั้นไม่ถูกต้อง

หนึ่งในตัวอย่างมาตรฐานที่ใช้อธิบายทฤษฎีบทของเบย์คือแนวคิดของการทดสอบโรค: ถ้าคุณทำการทดสอบที่ถูกต้อง 95% สำหรับโรคที่ 1 ใน 10,000 ของประชากรมีและคุณทดสอบบวกสิ่งที่เป็นไปได้ คุณเป็นโรคนี้หรือไม่?

คำตอบที่ไร้เดียงสาคือ 95% แต่การเพิกเฉยต่อปัญหาที่ 5% ของการทดสอบใน 9999 จาก 10,000 คนจะให้ผลบวกที่ผิดพลาด ดังนั้นโอกาสที่คุณจะเป็นโรคนี้ต่ำกว่า 95%

ฉันใช้วลีที่คลุมเครือ "โอกาสคืออะไร" โดยเจตนา ในการใช้ภาษาที่น่าจะเป็น / โอกาสที่น่าจะเป็น: ความน่าจะเป็นที่การทดสอบนั้นถูกต้องคือ 95% แต่สิ่งที่คุณต้องการรู้คือโอกาสที่คุณเป็นโรค

ปิดหัวข้อเล็กน้อย: ตัวอย่างคลาสสิกอื่น ๆ ที่ทฤษฎีบทของเบย์ใช้ในการแก้ปัญหาในหนังสือเรียนทั้งหมดคือปัญหามอนตี้ฮอลล์: คุณกำลังอยู่ในรายการคำถาม มีรางวัลหลังหนึ่งในสามประตู คุณเลือกหนึ่งประตู เจ้าภาพเปิดประตูสามเพื่อไม่เปิดเผยรางวัล คุณควรจะเปลี่ยนไปเป็นประตูสองที่ได้รับโอกาสหรือไม่

ฉันชอบการอ้างอิงใหม่ของคำถาม (ได้รับความอนุเคราะห์จากการอ้างอิงด้านล่าง): คุณอยู่ในรายการคำถาม มีรางวัลหลังหนึ่งในล้านประตู คุณเลือกหนึ่งประตู เจ้าภาพเปิดประตูอื่น ๆ ทั้งหมดยกเว้นประตู 1,04632 เพื่อไม่เปิดเผยรางวัล คุณควรเปลี่ยนเป็นประตู 104632 หรือไม่?

หนังสือเล่มโปรดของฉันที่กล่าวถึงทฤษฎีบทของเบย์มากจากมุมมองของเบย์คือ "ทฤษฎีข้อมูลการอนุมานและการเรียนรู้อัลกอริทึม" โดย David JC MacKay มันเป็นหนังสือสำนักพิมพ์มหาวิทยาลัยเคมบริดจ์, ISBN-13: 9780521642989 คำตอบของฉันคือ (ฉันหวัง) การกลั่นประเภทของการอภิปรายที่เกิดขึ้นในหนังสือเล่มนี้ (ใช้กฎตามปกติ: ฉันไม่มีส่วนเกี่ยวข้องกับผู้แต่งฉันชอบหนังสือเล่มนี้)

ทฤษฎีบทของเบย์ในรูปแบบที่ชัดเจนที่สุดคือการประกาศสองสิ่งใหม่:

1. $P(HD|I)=P(DH|I)$
2. $P(HD|I)=P(H|I)P(D|HI)$

ดังนั้นโดยใช้สมมาตร:

$P(D|I) \neq 0$$P(D|I)$

ดังนั้นนี่คืออะไร บางสิ่งบางอย่างที่เรียบง่ายช่างน่ากลัวเหลือเกิน เช่นเดียวกับสิ่งต่าง ๆ ส่วนใหญ่ "มันคือการเดินทางที่สำคัญกว่าจุดหมายปลายทาง" ทฤษฎีบทของเบย์สั่นสะเทือนเพราะข้อโต้แย้งที่นำไปสู่

$P(H|I)=1-P(\overline{H}|I)$

ตอนนี้ "กฎ" ในตรรกะการอนุมานคือถ้าคุณมีความสัมพันธ์ "A หมายถึง B" แล้วคุณยังมี "Not B หมายถึงไม่ A" ดังนั้นเราจึงมี "การใช้เหตุผลที่สอดคล้องกันแสดงถึงทฤษฎีบทของเบย์" ซึ่งหมายความว่า "ทฤษฎีบทของ Not Bayes แสดงถึงการให้เหตุผลที่ไม่สอดคล้องกัน" เช่นถ้าผลลัพธ์ของคุณไม่เท่ากับผลเบย์ในบางช่วงเวลาและโอกาสที่เป็นไปได้คุณจะให้เหตุผลที่ไม่สอดคล้องกัน

ผลลัพธ์นี้เรียกว่าทฤษฎีบทของ Cox และได้รับการพิสูจน์ใน "Algebra of Probable inference" ในปี 1940 ความน่าจะเป็นที่ได้รับล่าสุดในทฤษฎี Proability: ตรรกะของวิทยาศาสตร์

ฉันชอบคำนำของ Kevin Murphy สำหรับ Bayes Theorem http://www.cs.ubc.ca/~murphyk/Bayes/bayesrule.html

อ้างจากบทความนักเศรษฐศาสตร์:

http://www.cs.ubc.ca/~murphyk/Bayes/economist.html

สาระสำคัญของวิธีการแบบเบย์คือการให้กฎทางคณิตศาสตร์ที่อธิบายว่าคุณควรเปลี่ยนความเชื่อที่มีอยู่ของคุณในแง่ของหลักฐานใหม่ มันช่วยให้นักวิทยาศาสตร์รวมข้อมูลใหม่กับความรู้หรือความเชี่ยวชาญที่มีอยู่ ตัวอย่างที่เป็นที่ยอมรับคือการจินตนาการว่าทารกแรกเกิดที่แก่แดดสังเกตพระอาทิตย์ตกครั้งแรกของเขาและสงสัยว่าพระอาทิตย์จะขึ้นอีกครั้งหรือไม่ เขากำหนดความน่าจะเป็นก่อนหน้านี้ให้เท่ากันทั้งสองผลลัพธ์ที่เป็นไปได้และแสดงถึงสิ่งนี้โดยการวางหินอ่อนสีขาวหนึ่งก้อนและหินอ่อนสีดำหนึ่งก้อนลงในถุง วันต่อมาเมื่อดวงอาทิตย์ขึ้นเด็ก ๆ ก็วางหินอ่อนสีขาวไว้ในถุง ความน่าจะเป็นที่หินอ่อนที่ดึงออกมาจากถุงจะเป็นสีขาว (เช่นระดับความเชื่อของเด็ก ๆ ในอนาคตของดวงอาทิตย์) จึงหายไปจากครึ่งถึงสองในสาม หลังจากพระอาทิตย์ขึ้นในวันถัดไป เด็กเพิ่มหินอ่อนสีขาวอีกอันและความน่าจะเป็น (และระดับความเชื่อ) เพิ่มขึ้นจากสองในสามเป็นสามในสี่ และอื่น ๆ ความเชื่อเริ่มแรกว่าดวงอาทิตย์มีแนวโน้มที่จะไม่เพิ่มขึ้นทุกเช้าถูกปรับเปลี่ยนให้กลายเป็นความแน่นอนที่ดวงอาทิตย์จะขึ้น