การจัดกึ่งกลางสร้างความแตกต่างใน PCA ได้อย่างไร (สำหรับการแยกย่อย SVD และ eigen)

การจัดกึ่งกลาง (หรือลบความหมาย) ข้อมูลของคุณมีความแตกต่างจาก PCA อย่างไร ฉันได้ยินมาว่ามันทำให้คณิตศาสตร์ง่ายขึ้นหรือป้องกันพีซีเครื่องแรกไม่ให้ถูกครอบงำด้วยค่าเฉลี่ยของตัวแปร แต่ฉันรู้สึกว่าฉันยังไม่สามารถเข้าใจแนวคิดได้อย่างมั่นคง

ตัวอย่างเช่นคำตอบยอดนิยมที่นี่ข้อมูลที่อยู่ตรงกลางกำจัดการสกัดกั้นในการถดถอยและ PCA ได้อย่างไร อธิบายวิธีที่การไม่อยู่ตรงกลางจะดึง PCA แรกผ่านจุดเริ่มต้นแทนที่จะเป็นแกนหลักของคลาวด์พอยต์ จากความเข้าใจของฉันเกี่ยวกับวิธีที่พีซีได้รับจาก eigenvectors เมทริกซ์ความแปรปรวนร่วมฉันไม่สามารถเข้าใจได้ว่าทำไมสิ่งนี้จึงเกิดขึ้น

ยิ่งกว่านั้นการคำนวณของฉันเองที่มีและไม่มีการกำหนดกึ่งกลางดูเหมือนจะไม่สมเหตุสมผล

พิจารณาดอกไม้ setosa ในirisชุดข้อมูลใน R. ฉันคำนวณค่าลักษณะเฉพาะและค่าลักษณะเฉพาะของเมทริกซ์ความแปรปรวนร่วมตัวอย่างดังนี้

data(iris)
df <- iris[iris$Species=='setosa',1:4]
e <- eigen(cov(df))
> e
$values
[1] 0.236455690 0.036918732 0.026796399 0.009033261

$vectors
            [,1]       [,2]       [,3]        [,4]
[1,] -0.66907840  0.5978840  0.4399628 -0.03607712
[2,] -0.73414783 -0.6206734 -0.2746075 -0.01955027
[3,] -0.09654390  0.4900556 -0.8324495 -0.23990129
[4,] -0.06356359  0.1309379 -0.1950675  0.96992969

ถ้าฉันจัดกลุ่มชุดข้อมูลไว้ที่กึ่งกลางก่อนฉันจะได้ผลลัพธ์เหมือนกันทุกประการ ดูเหมือนว่าจะค่อนข้างชัดเจนเนื่องจากการอยู่ตรงกลางไม่ได้เปลี่ยนเมทริกซ์ความแปรปรวนร่วมเลย

df.centered <- scale(df,scale=F,center=T)
e.centered<- eigen(cov(df.centered))
e.centered

prcompผลการทำงานในตรงรวมกัน eigenvalue-วิคเตอร์นี้เป็นอย่างดีทั้งชุดเป็นศูนย์กลางและ uncentered

p<-prcomp(df)
p.centered <- prcomp(df.centered)
Standard deviations:
[1] 0.48626710 0.19214248 0.16369606 0.09504347

Rotation:
                     PC1        PC2        PC3         PC4
Sepal.Length -0.66907840  0.5978840  0.4399628 -0.03607712
Sepal.Width  -0.73414783 -0.6206734 -0.2746075 -0.01955027
Petal.Length -0.09654390  0.4900556 -0.8324495 -0.23990129
Petal.Width  -0.06356359  0.1309379 -0.1950675  0.96992969

อย่างไรก็ตามที่ฟังก์ชั่นที่มีตัวเลือกเริ่มต้นprcomp center = TRUEการปิดการใช้งานตัวเลือกนี้จะส่งผลให้พีซีที่ตามมาของข้อมูลที่ไม่มีการป้อน ( p.centeredยังคงเหมือนเดิมเมื่อcenterตั้งค่าเป็นเท็จ):

p.uncentered <- prcomp(df,center=F)
> p.uncentered
Standard deviations:
[1] 6.32674700 0.22455945 0.16369617 0.09766703

Rotation:
                    PC1         PC2        PC3         PC4
Sepal.Length -0.8010073  0.40303704  0.4410167  0.03811461
Sepal.Width  -0.5498408 -0.78739486 -0.2753323 -0.04331888
Petal.Length -0.2334487  0.46456598 -0.8317440 -0.19463332
Petal.Width  -0.0395488  0.04182015 -0.1946750  0.97917752

ทำไมสิ่งนี้จึงแตกต่างจากการคำนวณค่าไอเกนวีคเตอร์ของฉันเองในเมทริกซ์ความแปรปรวนร่วมของข้อมูลที่ไม่ได้ใส่ตัว มันต้องเกี่ยวข้องกับการคำนวณหรือไม่? ฉันเห็นแล้วว่าprcompใช้สิ่งที่เรียกว่าวิธี SVD มากกว่าการแยกย่อยค่าเฉพาะเพื่อคำนวณพีซี ฟังก์ชั่นprincompใช้หลัง prcompแต่ผลของมันจะเหมือนกับ ปัญหาของฉันเกี่ยวข้องกับคำตอบที่ฉันอธิบายไว้ที่ด้านบนของโพสต์นี้หรือไม่

$\bf X$ ${\bf X'X}/(n-1)$

— เซนิต
แหล่งที่มา

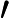
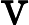
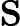
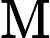
Based on my understanding of how the PC's are obtained from the covariance matrix's eigenvectors...โปรดอ่านความคิดเห็นในคำตอบที่คุณลิงค์ไป Covariances หมายถึงการจัดศูนย์กลางข้อมูลไว้ที่ PCA "on covariances" = PCA สำหรับข้อมูลกึ่งกลาง หากคุณไม่ได้จัดวางตัวแปรดั้งเดิมXไว้ PCA ที่ยึดตามข้อมูลดังกล่าวจะเป็น = PCA บนX'X/n [or n-1]เมทริกซ์ ดูภาพรวมยังมีความสำคัญ: stats.stackexchange.com/a/22520/3277

— ttnphns

through the origin, rather than the main axis of the point cloud. PCA เจาะแหล่งกำเนิดเสมอ ถ้าข้อมูลอยู่กึ่งกลางให้กำเนิด = เซนทรอยด์

— ttnphns

X^{'} X

$\bf X'X$

S

$\bf S$

ดูการวิเคราะห์องค์ประกอบหลัก: การทบทวนและการพัฒนาล่าสุดสำหรับการสนทนาของ PCA ที่อยู่กึ่งกลางและกึ่งกลาง (ซึ่งโดยทั่วไปจะไม่เหมือนกัน)

— Yibo Yang

D a t a \to Covariance matrix \to Eigen-decomposition,

$\mathrm{Data}\to\text{Covariance matrix}\to\text{Eigen-decomposition},$

[Wikipedia:] เพื่อหาแกนของวงรีเราจะต้องลบค่าเฉลี่ยของตัวแปรแต่ละตัวออกจากชุดข้อมูลเพื่อให้ข้อมูลอยู่กึ่งกลางจุดกำเนิด จากนั้นเราคำนวณเมทริกซ์ความแปรปรวนร่วมของข้อมูล ...

และคุณมีสิทธิ์ที่จะสังเกตว่านี่ไม่ใช่สูตรที่แม่นยำมาก

$\mathbf X^\top \mathbf X/(n-1)$ $\mathbf X$

Data X \to Matrix X^{⊤} X / (n - 1) \to Eigen-decomposition,

$\text{Data } \mathbf X\to\text{Matrix } \mathbf X^\top \mathbf X/(n-1)\to\text{Eigen-decomposition},$

จากนั้นการอยู่ตรงกลางมีความสำคัญมากและมีผลกระทบที่อธิบายและแสดงโดย @ttnphns ในการทำให้ข้อมูลถูกกำจัดจุดตัดในการถดถอยและ PCA ได้อย่างไร

$\mathbf X$

Data X \to Singular value decomposition .

$\text{Data } \mathbf X \to \text{Singular value decomposition}.$

$\mathbf X$ svd

— อะมีบาพูดว่า Reinstate Monica
แหล่งที่มา

ฉันมีคำแนะนำสำหรับคำตอบของคุณในการสร้างตรรกะที่สะอาดตา เนื่องจากในสองตัวอย่างแรก (eigen) ของคุณคุณกำลังพูดถึงเมทริกซ์การสลายตัว MSCP X'X/(n-1)และไม่ใช่เมทริก SSCP X'X- มันจะเป็นในตัวอย่าง svd แสดงให้เห็นถึงความเท่าเทียมกันในการย่อยสลายX/sqrt(n-1)แทนX(ตามที่คุณพูดในปัจจุบัน) [แน่นอนความแตกต่างนั้นมีเฉพาะในส่วนของสเกล (eigenvalues) ไม่ใช่ eigenvectors แต่มันก็เป็นการดีกว่าฉันคิดอย่างนั้นจริง ๆ ] ประเด็นที่สองของฉันคือการเตือนว่าเมื่อศูนย์กลางของXการแก้ไข Bessel n-1ไม่จำเป็นnยินดีต้อนรับ

— ttnphns

ทั้งข้อดีและข้อเสีย @ttnphns ฉันจะคิดว่าฉันจะรวมคำตอบเหล่านี้อย่างไร: ฉันต้องการคำตอบนี้ให้ผู้ชมเข้าใจได้กว้างขึ้นและพยายามหลีกเลี่ยงการเข้าไปในรายละเอียดทางคณิตศาสตร์ที่ไม่จำเป็น

— อะมีบาพูดว่า Reinstate Monica