สมมติว่าตัวแปรนั้นเป็นค่าบวกหรือไม่ใช่ลบขอบของขอบเป็นเพียงจุดที่เกินกว่าที่ข้อมูลจะกลายเป็น 0 หรือลบตามลำดับ เนื่องจากข้อมูลในชีวิตจริงมีแนวโน้มที่จะเอียงขวาเราจะเห็นความหนาแน่นของจุดมากขึ้นเมื่อการกระจายต่ำสุดและจึงมีความหนาแน่นมากขึ้นที่ "จุด" ของลิ่ม
โดยทั่วไปแล้ว PCA เป็นเพียงการหมุนของข้อมูลและข้อ จำกัด ของข้อมูลเหล่านั้นโดยทั่วไปจะปรากฏในองค์ประกอบหลักในลักษณะเดียวกับที่แสดงในคำถาม
นี่คือตัวอย่างการใช้ตัวแปรที่กระจายแบบล็อกทั่วไปหลายตัว:
library("vegan")
set.seed(1)
df <- data.frame(matrix(rlnorm(5*10000), ncol = 5))
plot(rda(df), display = "sites")

ขึ้นอยู่กับการหมุนโดยนัยของพีซีสองเครื่องแรกคุณอาจเห็นลิ่มหรือคุณอาจเห็นรุ่นที่แตกต่างกันบ้างแสดงที่นี่ในรูปแบบ 3 มิติโดยใช้ ( ordirgl()แทนplot())

ที่นี่ในแบบ 3 มิติเราเห็นหนามแหลมหลายอันยื่นออกมาจากมวลศูนย์กลาง
สำหรับตัวแปรสุ่มแบบเกาส์ (Xผม∼ ( N) ( μ = 0 , σ= 1 )) ที่แต่ละแห่งมีค่าเฉลี่ยและความแปรปรวนเหมือนกันเราจะเห็นขอบเขตของคะแนน
set.seed(1)
df2 <- data.frame(matrix(rnorm(5*10000), ncol = 5))
plot(rda(df2), display = "sites")


และสำหรับตัวแปรสุ่มที่เป็นบวกอย่างสม่ำเสมอเราจะเห็นลูกบาศก์
set.seed(1)
df3 <- data.frame(matrix(runif(3*10000), ncol = 3))
plot(rda(df3), display = "sites")


โปรดสังเกตว่าที่นี่สำหรับภาพประกอบฉันแสดงชุดเครื่องแบบโดยใช้ตัวแปรสุ่มเพียง 3 ตัวซึ่งคะแนนจะอธิบายลูกบาศก์ในรูปแบบ 3 มิติ ด้วยขนาดที่สูงขึ้น / ตัวแปรอื่น ๆ เราไม่สามารถแสดงไฮเปอร์คิวบ์ 5d ได้อย่างสมบูรณ์แบบในแบบ 3 มิติและด้วยเหตุนี้รูปร่าง "คิวบ์" ที่แตกต่างกันจึงผิดเพี้ยนไปบ้าง ปัญหาที่คล้ายกันมีผลต่อตัวอย่างอื่น ๆ ที่แสดง แต่ก็ยังง่ายที่จะเห็นข้อ จำกัด ในตัวอย่างเหล่านั้น
สำหรับข้อมูลของคุณการเปลี่ยนแปลงการบันทึกของตัวแปรก่อน PCA จะดึงส่วนท้ายและขยายข้อมูลที่เป็นกลุ่มเช่นเดียวกับที่คุณอาจใช้การแปลงดังกล่าวในการถดถอยเชิงเส้น
รูปร่างอื่น ๆ สามารถปลูกพืชในแปลง PCA; หนึ่งรูปร่างดังกล่าวเป็นสิ่งประดิษฐ์ของการแสดงตัวชี้วัดเก็บรักษาไว้ใน PCA และเป็นที่รู้จักในฐานะเกือกม้า สำหรับข้อมูลที่มีการไล่ระดับสีที่ยาวหรือเด่นชัด (ตัวอย่างที่จัดเรียงตามมิติเดียวที่มีตัวแปรเพิ่มขึ้นจาก 0 ถึงสูงสุดแล้วลดลงอีกครั้งเป็น 0 ตามส่วนของข้อมูลที่เป็นที่รู้จักกันดีในการสร้างสิ่งประดิษฐ์ดังกล่าวพิจารณา
ll <- data.frame(Species1 = c(1,2,4,7,8,7,4,2,1,rep(0,10)),
Species2 = c(rep(0, 5),1,2,4,7,8,7,4,2,1, rep(0, 5)),
Species3 = c(rep(0, 10),1,2,4,7,8,7,4,2,1))
rownames(ll) <- paste0("site", seq_len(NROW(ll)))
matplot(ll, type = "o", col = 1:3, pch = 21:23, bg = 1:3,
ylab = "Abundance", xlab = "Sites")

ซึ่งก่อให้เกิดรูปเกือกม้าสุดขั้วซึ่งจุดที่ปลายสุดของแกนงอกลับเข้ากลาง

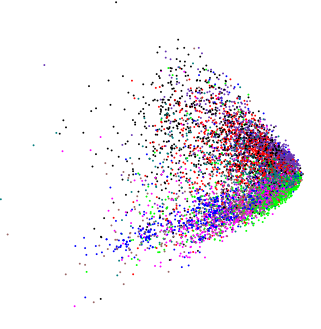 PCA):
PCA): (ยกเว้นในกรณีนี้ฉันอยากรู้ว่ามีโครงสร้างภายในหรือไม่)
(ยกเว้นในกรณีนี้ฉันอยากรู้ว่ามีโครงสร้างภายในหรือไม่)






